박사님이 주신 논문에서 HRV 특징 중 비선형 특징은 위 논문을 참고해서 진행하였다고 해서 한 번 읽어보려고 한다.
자발적으로 내가 찾은 첫 논문 ㅋ
싸이월드 파니룸 파도타기 쌉고수 실력 논문에도 적용해보겠습니더

실제 스트레스 감지를 위한 비선형 심박수 변화 기능(사례 연구: 대학 시험으로 인해 스트레스를 받는 학생들)
배경
HRV는 심장 박동(RR 간격) 사이의 시간에 따른 변화를 반영하는 비침습적 측정 방법이며, ANS(자율신경계) 활동의 신뢰할 수 있는 지표인 것으로 입증되었다.
이 연구에서 대학 시험으로 인해 스트레스를 받는 대상에서 가장 일반적인 비선형 HRV 측정이 어떻게 달라지는지 조사하고, 비선형 HRV 특성을 기반으로 스트레스를 자동 감지하는 분류기를 제안하려고 한다.
지속적인 언어 시험(스트레스)세션과 휴일 세션으로 나눠 피실험자의 ECG 기록에서 추출한 5분 HRV를 조사하였다.
여기서 잠깐!
선형 분석과 비선형 분석은 뭘까?
선형 분석: 시간이나 주파수 영역에서 심박동 간의 평균이나 표준편차와 같은 통계적 척도를 사용한다. 이는 데이터를 일정한 비율로 변화하는 패턴으로 간주하는데, 이 방식은 특정한 단순한 패턴을 설명하는 데 적합하다.
비선형 분석: 데이터가 단순한 비율로 변화하지 않고, 복잡한 패턴을 보일 때 이를 분석하는 방법이다. 비선형 분석에서는 카오스 이론, 프랙탈 분석과 같은 기법을 사용해 심박동 간의 복잡한 변동성을 측정한다.
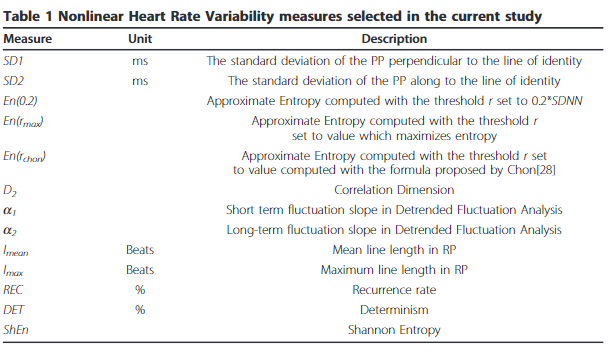
비선형 HRV 지표들
- Sample Entropy (SampEn): 심박동 시계열의 복잡성을 측정하는 지표로, 낮은 값은 데이터가 덜 복잡하고 예측 가능하다는 것을 의미하고, 높은 값은 복잡하고 예측하기 어렵다는 것을 나타낸다.
- Approximate Entropy (ApEn): 시계열의 복잡성을 나타내며, 데이터의 패턴이 얼마나 복잡하게 변화하는지를 측정한다.
- Poincaré Plot 분석 (SD1, SD2): RR 간격의 비선형 특성을 시각화하는 방법으로, SD1은 단기적 변동성을, SD2는 장기적 변동성을 나타낸다.
- Fractal Dimensions (D2): 시계열 데이터의 프랙탈 특성을 분석하여 심장의 복잡성을 측정한다. (프랙탈(Fractal)은 복잡한 구조가 반복되는 자기유사성(self-similarity)을 특징으로 하는 기하학적 형태)
위 논문에서 QRS 탐지기를 사용하여 RR 간격을 추출하고, 비선형 스케일링 방법을 사용하여 ECG 신호의 길이 특징을 분석했다. 두 명의 연구자가 QRS 탐지를 독립적으로 검토하고 교정하여 정상적인 박동 NN을 수동으로 레이블링하여 NN 시리즈를 만들었고, NN/RR 비율을 계산하였다.
(NN/RR 비율이 90% 미만인 데이터는 분석에서 제외될 수 있으나 이 연구에서는 모든 데이터가 90% 이상)
NN/RR이 필요한 이유는 NN 간격을 통해 비정상적인 박동은 제외되므로 NN/RR이 높으면 높을수록 정상적인 박동만을 고려한 것이기 때문에 정상적인 심장 활동을 기반으로 분석할 수 있다. 즉, 데이터의 신뢰성 및 정확한 HRV를 분석할 수 있다.
Poincaré Plot
푸앵카레 도표(PP)는 HRV를 시각화하기 위한 비선형분석 기법으로 연속적인 RR 간격 사이의 상관 관계를 나타내는 그래픽 표현이다. 두 RR 간격을 2차원 평면에 점으로 나타내며, 이를 통해 심장 박동 간 변동 패턴을 직관적으로 확인할 수 있다.(X축: 현재 RR 간격, Y축: 다음 RR 간격)

점들이 좁고 일직선에 가까울 때: 심장 박동 간격이 규칙적이고 변동성이 적다. 이는 스트레스 상태나 질병에서 흔히 나타납니다.
점들이 퍼져 있고 분포가 넓을 때: 심박 변동이 크고, 이는 건강한 상태에서 일반적으로 나타난다. 심박동이 다양한 환경에 적응하는 능력이 좋다는 것을 의미한다.(변동성이 크다는 것이니까 건강하다는 것)
Approximate entropy
근사 엔트로피(Approximate Entropy, ApEn)는 HRV(Heart Rate Variability) 분석에서 자율 신경계의 변동성을 측정하는 방법 중 하나로 시계열 데이터의 불규칙성을 측정한다. 데이터가 얼마나 예측하기 어려운지를 나타내며, 데이터의 복잡성과 패턴의 다양성을 평가한다. ApEn이 낮으면 시계열이 규칙적이고 예측하기 쉽지만, 높으면 시계열이 더 불규칙하고 예측하기 어려운 것을 의미한다.


RR 간격 데이터 RR1,RR2...가 주어지면 길이 m의 벡터를 생성하고, 벡터 Xi와 Xj 간의 거리를 정의한다. 이 거리는 벡터의 각 요소 간의 최대 절대 차이로 계산된다. 각 벡터 Xi에 대해, 벡터 Xj 중에서 거리 d[Xi,Xj]가 주어진 임계값 r 이하인 벡터의 비율을 계산하고 이 비율을 C_m_i(r)로 표현한다.
(예를 들어, 만약 10개의 벡터가 있고, 특정 벡터 Xi와 거리 r 이하인 벡터가 6개 있다면, 이 벡터에 대한 비율은 6/9
m과 r에 대한 C_m_i(r)의 평균값을 사용하여 ApEn을 게산한다.
(평균값은 데이터의 패턴이 얼마나 규칙적인지를 나타내는 지표임. 즉, C_m_i(r)는 특정 벡터 Xi와 비슷한 벡터들의 비율을 나타내고, 이 값을 모든 벡터에 대해 평균을 내면 데이터 전체의 규칙성을 평가할 수 있음)
-> C_m_i(r) 값이 높으면 데이터는 규칙적이라고 할 수 있음
-> ApEn은 길이 m의 벡터와 길이 m+1의 벡터에 대해 C_m_i(r)과 c_m+1_i(r)의 비율 차이임. 벡터의 길이를 늘렸을 때 비율이 급격히 변한다는 것이고, 즉 비율 차이가 크면 데이터의 패턴이 더 복잡하고 예측하기 어려운 것.
이 연구에서는 근사 엔트로피(ApEn)를 계산할 때 m=2를 사용하고, 임계값 r에 대해 세 가지 다른 값을 적용했다.
1. r = 0.2 x SDNN(NN의 표준편차)
-> HRV을 나타내는 시계열의 느린 동적 특성에 적합하다고 권장되는 방법
2. r = rmax
-> r의 범위 (0.1 x SDNN, 0.9 x SDNN)에서 근사 엔트로피를 최대화하는 r값
-> 데이터의 복잡성을 최대한 반영할 수 있도록 r값을 선택하는 방법
3. r=rchon

(N은 NN 시퀀스 길이, SDDS는 RRi+1 - RRi 차이값의 표준편차, SDNN은 NN의 표준편차)
Correlation Dimension
상관차원은 시계열의 복잡성을 평가하거나 비선형 동역학을 분석하고 패턴을 이해할 수 있는 중요한 분석 방법이다.
상관 차원 D2는 시계열의 복잡성을 측정하는 지표로, 시계열 데이터의 구조적 특성을 나타낸다.


Detrended Fluctuation Analysis(DFA)
비트렌디드 플럭투에이션 분석은 시계열 데이터의 상관관계를 평가하고 변동성 이해 및 서로 다른 시간 스케일의 패턴을 분석할 수 있고, 비선형 데이터를 처리할 수 있다. 즉, DFA는 신호 내의 상관관계를 측정하는 방법이다.

통합된 시계열을 같은 길이의 겹치지 않는 세그먼트로 나누고, 각 세그먼트에 대해 최소 제곱선을 맞춘다.
이 선을 yn(k)라고 한다.
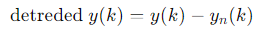
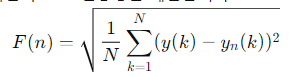
Recurrence Plot(RP)라는 또 다른 비선형 시계열 데이터의 복잡성을 측정하는 방법이 있는데 뇌 저장공간이 가득 차서 받아들일 수가 없다. 이건 과감히 패스!
그래서 이 복잡하고 난해한 수식들과 방법은 비선형 데이터를 분석하는 다양한 방법이다.
상관 차원은 데이터의 복잡성을 측정하고, 비선형 동역학을 분석한다. 데이터의 구조적 특성을 이해하는데 유용하다.
DFA는 시간 시계열의 상관관계를 평가하고, 장기 및 단기적 변동성을 분석한다. 데이터에서 트렌드를 제거하고 진정한 변동성을 측정한다.
근사 엔트로피는 데이터의 복잡성과 규칙성을 평가한다. 특정 패턴이나 규칙이 얼마나 예측하기 어려운지를 나타낸다.
분류 방법으로 LDA(Linear Discriminant Analysis)분석을 채택했다.
LDA는 여러 클래스의 데이터를 구분하기 위해 사용되며, 각 클래스 간의 분산을 최대화하고 클래스 내의 분산을 최소화하는 방향으로 데이터를 변환하여 분류 경계를 만든다.
각 클래스의 평균과 공분산을 사용하여 판별 함수를 생성하고, 이 함수는 주어진 입력 데이터가 어떤 클래스에 속하는지를 예측하는데 사용된다.
고차원 데이터를 저차원 공간으로 투영하여 차원을 축소하며, 이 과정에서 분류 성능을 극대화할 수 있도록 설계된다.
각 클래스의 데이터가 다변량 정규 분포를 따른다고 가정하며, 클래스 간 공분산이 동일하다고 가정한다.
| 실제 값 / 예측 값 | 양성(Positive) | 음성(Negative) |
| 양성(Positive) | TP(참 양성) | FN(거짓 음성) |
| 음성(Negative) | FP(거짓 양성) | TN(참 음성) |
(FP면 양성으로 잘못 분류됨, 원래는 음성임 <- 이렇게 해석)
1. 총 분류 정확도 (Accuracy, ACC)
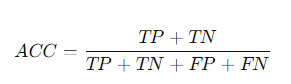
2. 민감도 (Sensitivity, SEN)
실제 양성 샘플 중에서 올바르게 양성으로 분류된 샘플의 비율
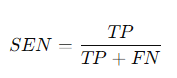
3. 특이도 (Specificity, SPE)
실제 음성 샘플 중에서 올바르게 음성으로 분류된 샘플의 비율
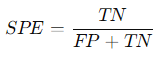
연구에서 13개의 HRV 특징을 사용하여 LDA를 적용할 수 있지만, 특징이 너무 많기 때문에 차원의 저주 문제로 인해 분류기의 성능이 저하될 수 있다.
(차원의 저주: 데이터 차원이 증가함에 따라 필요한 샘플 수가 기하급수적으로 증가하여 모델 성능이 떨어지는 현상)
두 클래스(스트레스, 휴식)간의 구분을 최대화하고 전체 분류 정확도를 높이고 가장 좋은 특징의 하위 집합을 찾기 위해 소진적 검색(exhaustive search)방법을 사용했다.
이 방법은 N개의 특징 중 k개를 선택하는 모든 조합을 조사한다. 즉 2^13=8192개의 특징 조합을 조사한다.
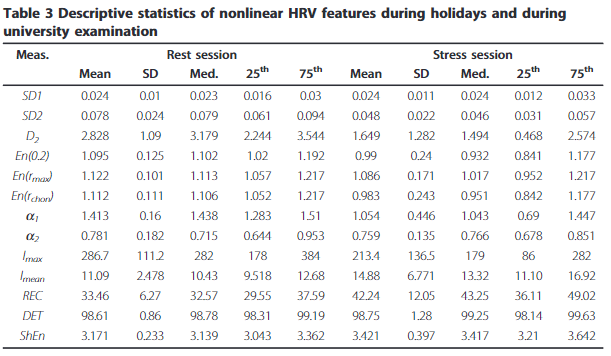
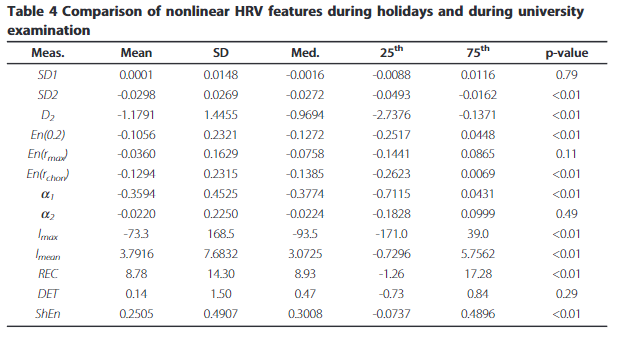
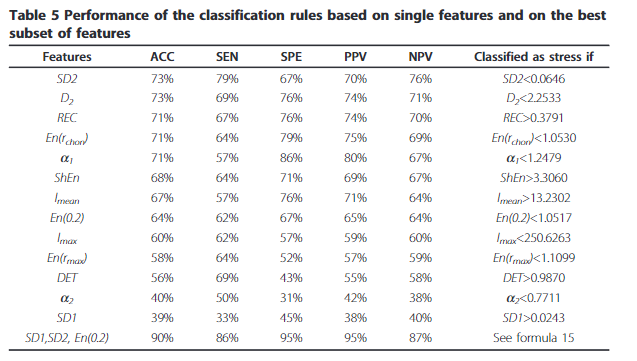
10겹 교차 검증을 통해 SD2와 D2가 가장 높은 분류 정확도를 보였다.
이진 분류로는 SD2가 0.0646ms보다 낮으면 스트레스 상태, 높으면 안정상태로 분류되고, REC, En(r chon), a1 기반의 분류기도 71%의 만족스러운 정확도를 나타냈다.
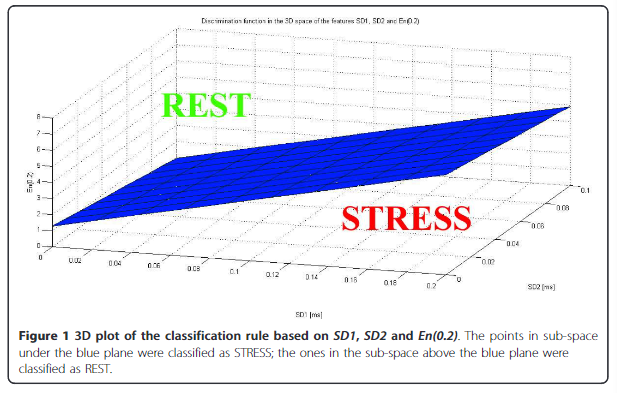
조합 분류로는 SD1, SD2, En(0.2)의 조합을 사용한 분류기가 90%의 총 분류 정확도를 나타냈다.
10.64 + 203.99 · SD1 − 108.74 · SD2 − 8.26 · En(0.2) > 0 이면 스트레스 상태로 분류한다.
결론
D2, En(0.2), En(r chon) 등 거의 모든 복잡성 측정값이 스트레스 세션동안 통계적으로 감소했다. 스트레스 상태에서 심박수가 더 안정적이고, 주기적인 행동을 보인다는 것으로 해석된다.(??? 일반적이지 않네)
D2와 En(r hcon)는 70% 이상의 총 분류 정확도로 스트레스를 감지하였고, SD2와 a1도 유사한 성능을 보였다.
SD1, SD2, En(0.2)로 구성된 조합이 90%의 분류 정확도를 보였다.
비선형 HRV 특성의 성능이 선형 HRV 특성보다 우수한 것으로 나타났다.

나는 어디. 여긴 누구?
미치겠네.. 먼소리고...
이 연구를 통해 그나마 이해한 것은 비선형 데이터의 복잡성을 분석하기 위해 근사 엔트로피, 상관차원, DFA라는게 있고..
근사 엔트로피(AnEp)는 클수록 복잡하고 예측하기 어려운 것이며.. PP라는 푸앵카레는 퍼져있을수록 건강한 것...
LDA는 다변량 정규분포를 가정하고, 클래스 간 공분산이 동일하다고 가정을 하는데 선형 판별 분석이다 보니 분석을 하면 선형 판별 함수가 생성되고, 그 함수로 클래스를 분류한다는 것...
건강하면 다양한 변수에 적응 및 대처할 수 있으니 다양하고 퍼져있다!!! 분산으로 치면 분산이 큰게 건강한 것!
왐시 어떡해
몰라
안녕
논문 전문: extension://bfdogplmndidlpjfhoijckpakkdjkkil/pdf/viewer.html?file=file%3A%2F%2F%2FC%3A%2FUsers%2Fbionics%2FDownloads%2F1475-925X-10-96%2520.pdf