순환신경망 RNN 모델은 짧은 시퀀스만 좋음
timesteps가 길어지면 앞의 정보가 뒤로 충분히 전달되지 못하는 현상 발생함
LSTM(Long Short-Term Memory) 모델

LSTM 모델은 은닉층의 메모리 셀에 삭제, 입력, 출력 게이트를 추가하여
불필요한 기억을 지우고 기억해야할 것들을 정함
긴 시퀀스 입력을 처리하는데도 성능이 굿
그래서 RNN 모델의 단점을 보완한 모델이래
삭제, 입력, 출력 게이트에는 공통적으로 시그모이드 함수가 존재함
시그모이드 함수를 지나면 0과 1 사이의 값이 나오게 되는데 이걸로 게이트를 조절함

입력 게이트
현재 정보를 기억하기 위한 게이트


위의 식은 t 시점의 입력값과 가중치 Wxi를 곱한 값과
t-1 시점의 은닉 상태와 가중치 Whi를 곱한 값을 더해서 시그모이드 함수를 지남 -> 0과 1 사이로 나옴
아래 식은 t 시점의 입력값에 가중치 Wxg를 곱한 값과
t-1 시점의 은닉 상태와 가중치 Whg를 곱한 값을 더해서 하이퍼볼릭탄젠트 함수를 지남 -> -1과 1 사이로 나옴
두 개의 값을 가지고 선택된 기억할 정보의 양을 정한다고 함(뒤에 설명)
삭제 게이트
기억을 삭제하기 위한 게이트
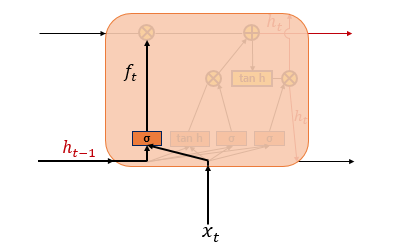

t 시점의 입력값과 t-1 시점의 은닉 상태가 시그모이드 함수를 지남 -> 0과 1 사이로 나옴
이 값이 삭제 과정을 거친 정보의 양임
0에 가까울수록 정보가 많이 삭제된 것이고
1에 가까울수록 정보가 온전히 기억한 것
이 값이 셀 상태(Cell State)에 곱해져 실제로 어떤 정보를 잊을지 결정됨
셀 상태(장기 상태)

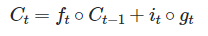
삭제 게이트에서 일부 기억을 잃은 상태라고 가정
입력 게이트에서 구한 it와 gt 두 개의 값에 대해서 원소별 곱(행렬곱)을 진행함
입력 게이트에서 선택된 기억을 삭제 게이트의 결과값과 더함
시점 t의 셀 상태를 의미하고 이 값을 시점 t+1의 LSTM 셀로 보냄
삭제 게이트의 출력값인 ft가 0이 되면 입력 게이트의 결과만 셀 상태값 Ct에 영향을 끼침
반대로 입력 게이트의 출력값인 it가 0이 되면 출력 게이트의 결과만 셀 상태값 Ct에 영향을 끼침
즉, 삭제 게이트는 이전 시점의 입력을 얼마나 반영할 것인지
입력 게이트는 현재 시점의 입력을 얼마나 반영할 것인지 결정함
출력 게이트와 은닉 상태(단기 상태)

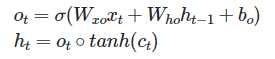
출력 게이트는 시점 t의 입력값과 시점 t-1의 은닉 상태가 시그모이드 함수를 지난 값
시점 t의 은닉 상태를 결정하는데 쓰임
GRU(Gated Recurrent Unit) 모델
업데이트 게이트와 리셋 게이트만 존재함
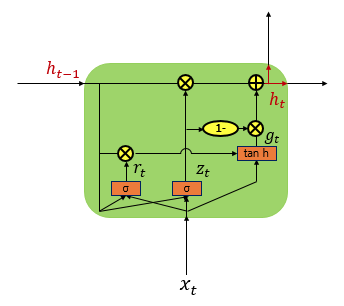
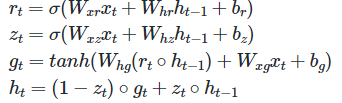

rt는 리셋 게이트고 zt는 업데이트 게이트임
rt가 0이면 완전히 잊는거를 의미함
zt 수식을 보면 새로운 정보를 얼마나 반영하고 과거 정보를 얼마나 유지하는지 결정함
gt는 중간 은닉 상태이고 ht는 최종 은닉 상태임
중간 은닉 상태는 과거 정보를 일부 삭제한 상태를 반영하여 계산된 값
GRU와 LSTM 중 어떤 것이 모델의 성능면에서 더 낫다라고 말할 순 없음
기존에 LSTM을 사용하면서 최적의 하이퍼파라미터를 찾아낸 상황이면 GRU 모델 필요없음
데이터 양이 적으면 GRU를 쓰고 데이터 양이 많으면 LSTM 추천
근데 지금 트랜스포머 나오면서 둘 다 안 쓸듯ㅋ 내 생각
드디어!!!! 내가 젤 궁금해했던
CNN(Convolution Neural Network) 합성곱 신경망

CONV는 합성곱 연산을 의미하고 연산의 결과가 활성화 함수 렐루를 지남 -> 이 과정이 합성곱층
POOL 구간은 풀링 연산을 의미 -> 풀링층
이미지는 (높이, 너비, 채널)이라는 3차원 텐서임
높이는 세로이고 너비는 가로, 채널은 색 성분을 의미함
흑백은 채널이 1이고 그 외의 색들은 R,G,B를 이용하기 때문에 채널이 3임
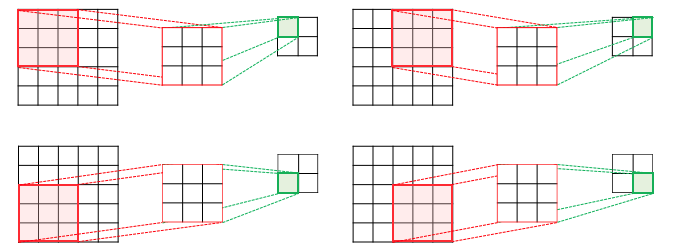
합성곱층은 합성곱 연산을 통해서 이미지의 특징을 추출하는 역할을 함
입력(빨간색)으로부터 커널(하얀색)을 사용하여 나온 결과(연두색)을 특성 맵이라고 함
그리고 커널의 이동 범위를 스트라이드(stride)라고 하는데 사용자가 정할 수 있음
합성곱 연산 결과로 얻은 특성맵은 입력보다 크기가 작아짐
합성곱 층을 여러개 쌓았다면 최종 특성맵은 초기 입력보다 매우 작아질 것임
특성 맵의 크기가 입력의 크기와 동일하게 유지되고 싶다???
패딩(padding) 써
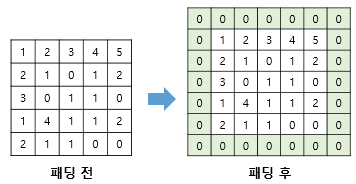
패딩은 합성곱 연산 전에 입력의 가장자리에 지정된 개수의 폭만큼 행과 열을 추가해주는 것
주로 0으로 채우는 제로 패딩(zero padding)을 사용함
지금까지는 채널을 고려하지 않고 2차원 텐서를 가정하고 설명함
하지만 실제로 합성곱 연산의 입력은 다수의 채널을 가진 경우가 많음
다수의 채널을 가진 입력 데이터면 커널의 채널 수도 입력의 채널 수만큼 존재해야함
머시고랭~~~~~~~~~~~~??????
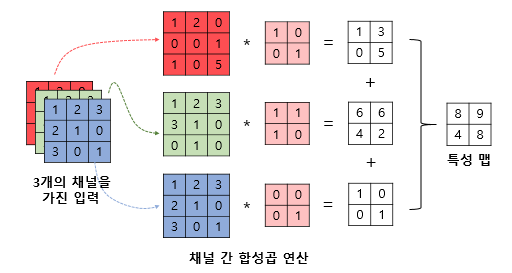
채널이 여러 개일 땐 각 채널 간 합성곱 연산을 마치고 그 결과를 모두 더해서
하나의 채널을 가지는 특성맵을 만듦
주의할 점은 연산에서 사용되는 커널은 3개의 커널이 아니라
3개의 채널을 가진 1개의 커널이래
-> 높이 3, 너비 3, 채널 3의 입력이 높이 2, 너비 2, 채널 3의 커널과 합성곱 연산을 해서
높이 2, 너비 2, 채널 1의 특성맵을 만든 것
합성곱층 공부 했으면 담으로는
풀링층(Pooling)
풀링층에서는 특성맵을 다운샘플링하여 특성맵의 크기를 줄이는 풀링 연산이 이루어짐
풀링 연산에는 최대 풀링(max pooling)과 평균 풀링(average pooling)이 사용됨
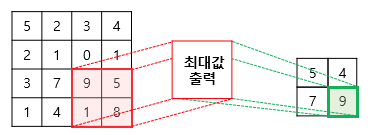
풀링 연산에서도 커널과 스트라이드 개념을 사용함
위의 사진은 스트라이드가 2인데 2x2 커널로 최대 풀링을 했을 때 특성맵이 절반의 크기로 다운샘플링됨
최대 풀링은 커널과 겹치는 영역 안에서 최대값을 추출하는 방식으로 다운생플링함
평균 풀링은 그럼 겹치는 영역 안에서 평균 계산하는 거겠지...
풀링은 합성곱 연산과 유사하지만 차이점이 있다면
학습해야 할 가중치가 없고 연산 후에 채널 수가 변하지 않음
'공부공부' 카테고리의 다른 글
| [딥러닝] 퍼셉트론, 기울기 소실 방지, 순환신경망 RNN모델 (0) | 2024.11.28 |
|---|---|
| [딥러닝] 혼동 행렬, 시그모이드 함수, 렐루 함수 등 (0) | 2024.11.26 |
| 2024 노벨 생리의학상 miRNA 유전자 조절 (4) | 2024.11.02 |
| 신호 처리를 위한 HPF 필터 (1) | 2024.10.10 |
| [Biopac] ECG(심전도), 신호 처리를 위한 LPF 필터에 대하여 (4) | 2024.09.23 |